K-Means Clustering using R

3 분 소요

caret 패키지

classification and regression training 의 약어로 복잡한 회귀와 분류 문제에 대한 모형 훈련(training)과 조절(tuning) 과정을 간소화하는 함수를 포함한다.
훈련데이터의 전처리, 변수의 중요성 계산 및 모형 시각화를 위한 방법을 포함한다.

caret 패키지 다운로드 & 사용

install.packages(“caret”) library(caret)

Console 창에 이 두줄 만 입력하면 다운로드하고 사용할 수 있다.

군집 vs 분류

군집(clustering) : 데이터 간의 유사도를 정의하고 그 유사도에 가까운 것부터 순서대로 합쳐가는 방법

군집 분석은 label 에 대한 정보를 모르기 때문에 각 개체가 어떤 군집에 들어갈까 예측하기 보단 이렇게도 나눠질 수 있구나 하는 정도의 지식을 발견
군집은 애초에 label가 없기 때문에 순수 데이터상의 특징으로 유사도를 정의하여 그룹을 만든다. 그렇기 때문에 군집 분석 방법에 따라 차이가 날 수 있다.
마케팅 조사에서 소비자들의 상품구매행동이나 life style에 따른 소비자군을 분류하여 시장 전략 수집 등에 활용한다.

분류(classification)

기존에 존재하는 데이터의 category 관계를 파악하고, 새롭게 관측된 데이터의 category를 스스로 판별하는 과정
미리 labeling 된 데이터들을 label 대로 분류하는 과정

비계층적 군집화(non-hierarchical clustering)

비계층적 군집방법은 정해진 개수로 군집을 나누는데, 정해진 기준에 따라 더 이상 개선이 되지 않을 때 까지 군집화를 진행한다.

비계층적 군집방법의 종류

1) K-means clustering : Centroid-based clustering
2) Expectation-Maximization(EM) clustering : Distribution-based clustering
3) Density-vased clustering
4) Fuzzy clustering : numeric variable 만 가능

K-Means Clustering

K-means Clustering : 주어진 군집 수 k에 대해서 군집 내 거리제곱합의 합을 최소화 하는것이 목적

즉 거리제곱합의 합이 군집화가 얼마나 잘됐는지 알려주는 척도가 됨.

K-Means Clustering의 특징

거리 계산을 통해 군집화가 이루어지므로 연속형 변수에 활용이 가능
K개의 초기 중심값은 임의로 선택 가능하며, 가급적이면 멀리 떨어지는 것이 바람직하며 초기 값을 일렬로 선택하지 않는 것이 좋다.
초기 중심으로부터의 오차의 제곱합을 최소화하는 방향으로 군집이 형성되는 탐욕적(greedy) 알고리즘이므로 안정된 군집은 보장하나 최적이라는 보장은 없다.

K-Means Clustering 장·단점

장점

간단한 원리

매우 유연하며 간단한 수정 가능

효율적인 군집화 가능

단점

초기 클러스터링 중심점에 매우 종속적

군집 갯수 선택에 대한 추측이 필요

군집 갯수에 대한 지식이 없다면 “데이터 수 (n) / 2” 의 제곱근으로 하거나 그래프를 그려 elbow point 로 선정

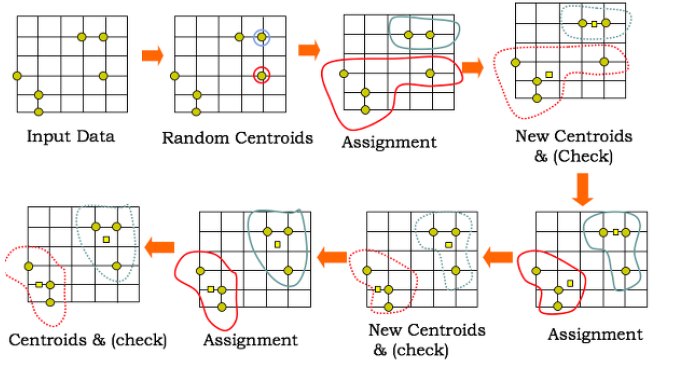
K-Means Clustering의 알고리즘

k값을 초기값으로 먼저 받고, 데이터를 k개의 초기 군집으로 나눔.
k개의 초기군집의 centroid(중심점)을 설정함.
각 데이터 개체와 현재 군집 중심점(centroid) 사이의 거리를 구함.
만약 개체가 현재 군집 평균에 가까우면 현재 소속군집에 포함하고 그렇지 않으면 다른 군집으로 재할당.
개별 군집의 평균이 다시 계산되어, 클러스터의 중심점(centroid)을 다시 계산.
반복하면서 클러스터가 더 이상 재지정 되는 점이 없으면 마침.

dist함수의 거리 유형

군집을 구별시켜줄 거리를 계산하는 ‘dist’함수

유클리드 거리 (default)
맨하탄 거리
표준화 거리
민콥스키거리

예제 : iris 데이터를 이용하여 K-means Clustering 실습

data(iris) head(iris)

Kmeans 군집 분석을 하기 위해 kmeans 함수를 사용

kmeans.iris <- kmeans(iris[,-5],3)

iris 데이터에서 species 열의 데이터를 제외한 나머지 열의 데이터들을 3개의 군집으로 분석하기 위하여 (iris[,-5],3) 이라는 매개변수 사용

iris 데이터의 Species에 3가지 군집이 있는 걸 알고 있기 때문에 k=3

군집 내 제곱합의 합을 최소화 하는게 군집화를 얼마나 잘 알려주는지에 대한 척도라고 하였기 때문에 이 값을 구해보겠다. withinss : 그룹 내 거리의 분산을 합한 것

군집 내 제곱합의 합을 최소화하는 값

round(sum(kmeans.iris$withinss),2)

각 데이터가 어떤 군집으로 분류되었는지 ‘cluster’ 로 확인

kmeans.iris$cluster

iris[,5] : 원래 데이터 확인 table(iris[,5],kmeans.iris$cluster) : 테이블로 비교

각 군집의 중심점 확인

kmeans.iris$center : 각 군집의 중심점 확인

시행횟수를 늘리는 방법

( 잘못된 군집화를 하는 경우 예측력을 늘리기 위해 )

kmeans10.iris <- kmeans(iris[,-5],3,nstart=10)

시행횟수를 10번으로 늘림

4차원의 데이터를 2차원으로 시각화 하기 위해 1,2열만 보기

plot(\iris[,1:2],pch=8,col=1:3,cex=2)

pch : 심볼 , col : 색 , cex: 크기

K-means clustering 에서 적당한 cluster 수 찾기

cluster 개수별로 k-means clustering 을 한 결과 도출된 tot.withinss 는 그룹 내 거리의 분산을 합한 것으로 얼마나 동질적인지 보여 준다. 따라서 동질적인 cluster 를 더 나눈다고 tot.withinss 는 크게 낮아지지 않는다. 이를 이용하여 tot.withinss가 급격히 낮아지는 한계를 적절한 cluster 개수로 판단하는 것이 적합하다.

visual <- NULL for(i in 2:6) { set.seed(0723) eval(parse(text=paste(“result”,i,”<- kmeans(iris[,-5],”,i,”);”,sep=””))) eval(parse(text=paste(“visual[“,i,”] <- result”,i,”$tot.withinss”,sep=””))) } plot(visual[-1], type=”l”, ylab=””, xlab=””, main=”cluster의 개수에 따른 내부분산”) abline(v=3,col=”red”)

Twitter Facebook LinkedIn