Single-layer Perceptron implements using Python
퍼셉트론이란?
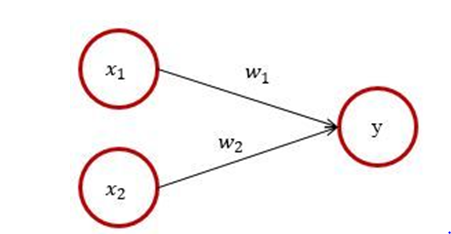
신경망(딥러닝)에 기원이 되는 알고리즘으로 다수의 input 을 받아서 하나의 출력을 한다. 뉴런이 전기신호를 내보내 정보를 전달하는 것과 비슷하게 보면 된다. 퍼셉트론이 동작하는 방식은 각 노드의 가중치와 입력치를 곱한 것을 모두 합한 값이 활성함수에 의해 판단되는데, 그 값이 임계치보다 크면 뉴런이 활성화 되고 결과값으로 +1을 출력한다. 그리고 뉴런이 활성화 되지 않으면 결과값으로 0을 출력한다.
단층 퍼셉트론
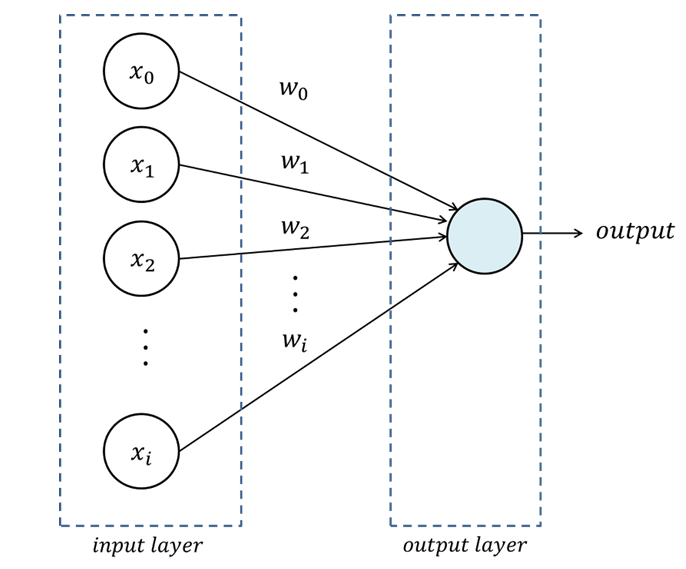
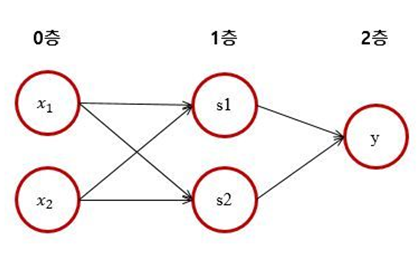
단층 퍼셉트론은 입력층(input layer)과 출력층(output layer)으로 구성된다. 입력층은 학습 벡터 또는 입력 벡터가 입력되는 계층으로써, 입력된 데이터는 출력층의 뉴런으로 전달되어 활성함수에 따라 값이 출력된다. 출력층은 퍼셉트론 설계 시 임의의 n개의 뉴런으로 구성할 수 있으며, 위의 그림은 한 개의 뉴런으로 구성된 출력층을 나타낸다. 단층 퍼셉트론의 대표적인 예시로는 AND 게이트이다. AND 게이트는 입력이 둘이고 출력이 하나인 대표적인 퍼셉트론이며 OR,NAND 등의 게이트 역시 나타낼 수 있다. 하지만 단층 퍼셉트론의 한계점은 XOR 게이트에서 보여지게 된다.
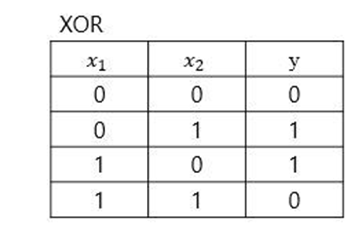
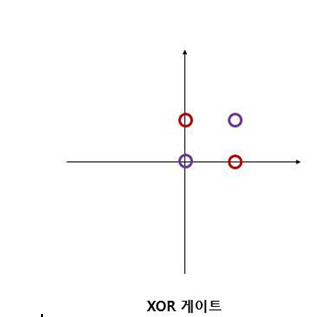
XOR 게이트는 배타적 논리합이라는 논리회로로 이는 선형적으로 나타낼 수 없다.
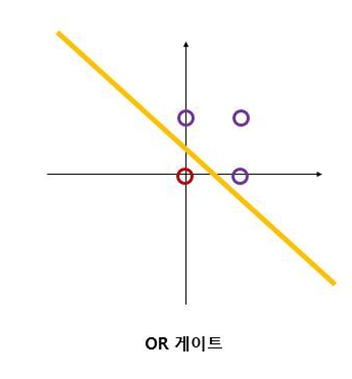
XOR 같은 경우에는 OR 게이트와 다르게 직선의 하나로 경우를 나눌 수 없게 된다. 이를 비선형적이라고 부르며 이것을 표현하기 위해 다층 퍼셉트론이 등장하게 된다.
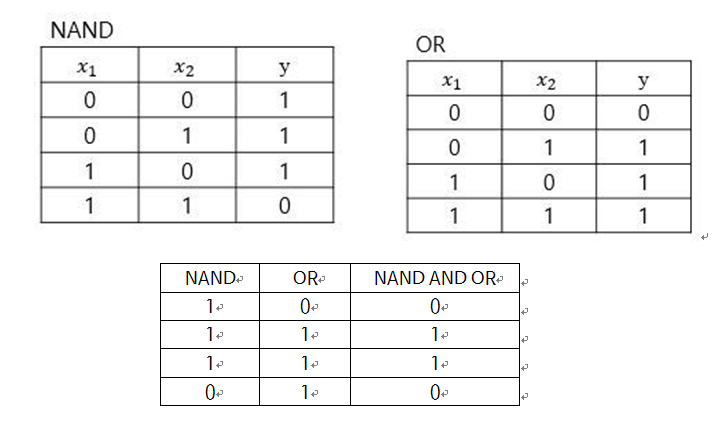
XOR게이트는 NAND 와 OR 을 AND 시키면 나오게 된다.
이를 단층 퍼셉트론으로 표현하지는 못하지만 다층 퍼셉트론(2층 퍼셉트론)으로는 표현할 수 있다.
하지만 이번 게시물에서는 단층 퍼셉트론만 다룰 예정이다.
소스 코드
코드 설명
(1) Main함수
코드는 크게 2가지 부분으로 나뉜다. 하나는 학습을 수행하는 fit 함수, 또 다른 하나는 테스트를 진행하는 predict 함수가 있다. 메인의 실행부터 먼저 보겠다.
clf = Perceptron() #학습을 수행한다. clf.fit(x,y) #테스트를 수행한다. print(clf.predict(x))
메인의 부분이다. 메인에서는 먼저 Perceptron 클래스의 객체를 생성하여 clf 변수에 할당한다. 즉 여기서 clf는 Perceptron 클래스의 객체가 되며, 이 Perceptron클래스 객체인 clf를 통해 Perceptron 클래스의 메소드인 fit 함수를 실행하여 학습을 진행하게 된다. 또한 이 학습이 끝나게 되면 predict 함수를 실행하여 올바르게 학습이 되었는지 테스트를 진행하게 되는 구조이다.
(2) 전역변수
x= [] d= [] #원하는 출력 y= [] b= 0.0 w0=0.0 #bias 기울기 w= [] eta=0.1
이 부분은 전역변수를 선언해 놓은 부분이다. 각 변수들은 클래스 내의 다른 메소드들에서도 사용되어야 하기 때문에 전역으로 선언해 주었다. 위에서부터 순서대로
- x : 2차원 리스트로 input 값 x1,x2 가 들어간다. 여기서는 이렇게 설정을 해 두었지만 실제 input 은 더 많을 수 있다.
- d : 1차원 리스트로 학습을 다 진행하였을 때, 나오길 원하는 답(문제의 실제 답)을 저장하는 리스트이다.
- y : 1차원 리스트로 학습을 진행하였을 때 실제로 나오는 값을 저장하는 리스트이다.
- b : 바이어스의 입력 값
- w0 : bias의 기울기 값이다
- w : 1차원 리스트로 ,각 input 들의 가중치 값이다. 이들은 input의 수와 동일한 개수의 크기를 가진다. 즉 input이 2개이면 가중치도 2개이다.
- eta : 학습율을 의미한다. 여기서 학습율은 0~1사이의 난수로 설정되는데 , 너무 크거나 너무 작으면 안되기 때문에 0.1로 설정했다.
(3) Perceptron 클래스의 생성자
def init(self):
global x,d,b,w,w0
x = [[0,0],[0,1],[1,0],[1,1]]
d= [0,0,0,1] #원하는 출력
b= -0.1 #초기 bias
w = [0,0]
w0 = 1.0
super().__init__()
메인에서 Perceptron 클래스의 객체를 만들 때의 생성자 부분이다. 이는 객체가 만들어질 때 자동으로 실행되며 객체들은 해당 값으로 초기화 된다. Global 변수로 선언되어져 있는 이유는 전역변수의 값을 변경해야 하기 때문이다.
(4) Perceptron 클래스의 학습함수(fit)
def fit(self,x,y):
global w,b
epoch = 0;
while True: #가중치가 변경되지 않을 때까지 반복
print("=======================================================================================================")
print("에포크 : ",epoch+1)
for i in range(len(d)):
net = (w[0]*x[i][0])+(w[1]*x[i][1])+(w0*b)
if net>=0.0:
f=1
else:
f=0
y.append(f)
if d[i]==y[i]: #학습 종료
print("x1:",x[i][0]," | x2:",x[i][1]," | 원하는 값 : ",d[i]," | 실제 값 : ",y[i],
" | 오차 : ",d[i]-y[i]," | bias :",round(b,2)," | w1 :",round(w[0],2)," | w2 :",round(w[1],2))
continue
else:
b=b+eta*(d[i]-y[i])*w0 #w0
w[0]=w[0]+eta*(d[i]-y[i])*x[i][0] #w1
w[1]=w[1]+eta*(d[i]-y[i])*x[i][1] #w2
print("x1:",x[i][0]," | x2:",x[i][1]," | 원하는 값 : ",d[i]," | 실제 값 : ",y[i],
" | 오차 : ",d[i]-y[i]," | bias :",round(b,2)," | w1 :",round(w[0],2)," | w2 :",round(w[1],2))
if d==y:
print("=======================================================================================================")
break
else:
y=[]
epoch=epoch+1
이 코드의 핵심이라고도 할 수 있는 학습 파트 부분의 함수이다. 학습 함수의 알고리즘에 대해서 먼저 설명을 하겠다. 퍼셉트론의 모델에서 각 입력이 들어갈 때 , 이 입력들에 대하여 해당하는 각각 가중치들을 곱하고 이 곱해진 값들을 다 더하며, 이 부분에 바이어스(임계값)를 더해준다. 바이어스(임계값)를 더하는 이유는 입력 값이 0인 경우에는 학습이 되지 않으며 들어오는 신호가 일정 이상이 되어야 활성화 함수가 활성화가 되어 학습이 진행될 수 있게 되기 때문에 이 바이어스 값을 더해준다. 정확하게는 바이어스가 학습데이터와 가중치가 계산되어 넘어야하는 임계점을 의미한다. 가중치는 입력신호가 결과 출력에 주는 영향도를 조절하는 매개변수이고, 바이어스는 뉴런이 얼마나 쉽게 활성화 되느냐를 조정하는 매개변수가 된다. 이 더해진 값들이 0보다 크거나 같으면 활성화(1)가 되고, 0보다 작으면 활성화가 되지 않는다(0). 여기서 각 입력들에 대한 활성화 함수의 결과값을 저장한 리스트(실제로 학습을 통해 나온 결과)와 나와야하는 예상 결과와 비교를 하여 만약 같다면 학습을 진행하지 않고, 다르다면 예상 결과와 같은 값이 나올 수 있도록 각 가중치의 값을 조절한다. 예를 들어 and 연산을 한다고 가정을 해보겠다. 각 입력에 대한 결과들은 아래의 표처럼 나온다.
| 입력1 | 입력2 | 결과 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
그럼 여기서 원래대로 나와야 할 결과 값은 [0,0,0,1] 이 된다. 이 학습 알고리즘에서는 각 입력들을 넣었을 때, 나와야 할 결과 값처럼 나와야 학습이 끝났다고 할 수 있다. 그렇기 때문에 학습 알고리즘에서는 각 입력을 넣었을 때 해당 결과가 나오도록 각 값들의 가중치와 바이어스를 조절하며 반복하는 것이라고 말할 수 있다. 이렇게 한 각 입력들에 대한 4개의 결과값이 나오면 이를 한 에포크(epoch) 라고 한다. 이 에포크는 학습이 끝날 때까지 계속해서 반복된다. 이 학습 메소드의 코드에서 실제로 나와야 할 결과 값은 리스트 변수 d로 선언되었고, 학습이 진행되었을 때마다 실제로 나오는 결과는 리스트 y, 각 입력들은 리스트 x, 입력들에 대한 각 가중치들은 w, 바이어스의 입력 값은 b, 바이어스의 기울기는 w0으로 선언하였다. 해당 코드에서는 하나의 학습 벡터[0,0]에 대한 뉴런의 net을 계산해야 하는데, 이 net은 각 입력들과 가중치의 내적을 한 값이다. 한마디로 각 가중치들과 각 입력들의 곱의 합을 의미한다. 이 net 값으로부터 활성함수를 통하여 뉴런의 실제 출력 값을 계산하며 만약 이 계산 결과 값이 0보다 크거나 같으면 1, 0보다 작으면 0이다. 이 각 각의 계산 결과 값은 리스트 y에 추가해주었다. 그런 다음, 이 결과 값이 실제 나와야 하는 결과와 비교를 하였을 때 같으면 해당 벡터에 대한 학습을 종료시키고, 그렇지 않으면 각 가중치들을 조정하며 이 학습 결과 값이 실제 원하는 결과 값과 같을 때까지 반복한다.
(5) Perceptron 클래스의 테스트함수
def def predict(self,x): list=[] for i in range(len(x)):
net = (w[0]*x[i][0])+(w[1]*x[i][1])+(w0*b)
if net>=0.0: list.append(1)
else:
list.append(0)
return list
Predict 함수는 테스트 부분이다. 실제로 학습이 종료되었을 때, 올바르게 학습이 되었는지 테스트하는 부분이다. Input 값을 넣었을 때, 나와야 하는 결과값과 같은 결과값들이 나온다면 이는 학습이 잘 됐다고 볼 수 있다.
결과
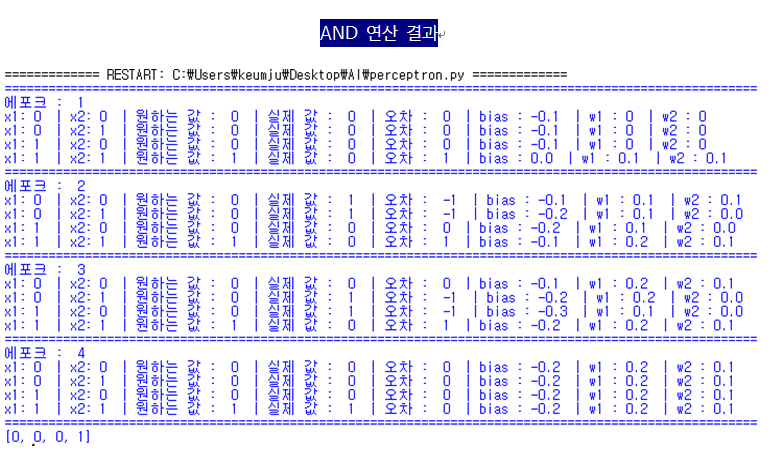
위의 코드는 AND 연산을 진행한 부분이고 , 이에 대한 결과는 아래와 같다.
OR 연산
def init(self):
global x,d,b,w,w0
x = [[0,0],[0,1],[1,0],[1,1]]
d= [0,1,1,1] #원하는 출력
b= -0.1
w = [0,0]
w0 = 1.0
super().__init__()
XOR 연산
def init(self):
global x,d,b,w,w0
x = [[0,0],[0,1],[1,0],[1,1]]
d= [0,1,1,0] #원하는 출력
b= -0.1
w = [0,0]
w0 = 1.0
super().__init__()